Orta Çağ’ın en büyük matematikçilerinden birisi olan Fibonacci’nin en derin bulgularından birisi de şüphesiz herkesin bir şekilde adını duyduğu Fibonacci dizisidir. Fibonacci dizisindeki sayılar doğadaki bir çok fenomen ile birebir örtüştüğü için insanı garip düşüncelere sürükler.

Fibonacci dizisi denilen sayılar şöyle başlar ve sonsuza dek gider:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …

Bu sayıları üreten fonksiyonu daha önceden bilmiyorsanız dahi şöyle bir bakarak kolayca her bir sayının kendisinden önceki iki sayının toplamı olduğunu görebilirsiniz. Ayrıca sayılar arasındaki orana pi ve e gibi bir sabit olan altın oran denir ve bu sabit ile kriptografik algoritmalardan tutun da rönesans dönemi mimari ve sanat eserlerine kadar bir çok yerde karşılaşmak mümkündür.

Doğada fibonacci sayıları o kadar çok yerde gözlemlenebilir ki “bu sayılarda bir iş var hocam” dememek elde değildir. İlginizi çekiyorsa bunu araştırmayı size bırakıyorum. Buradan ya da buradan başlayabilirsiniz.

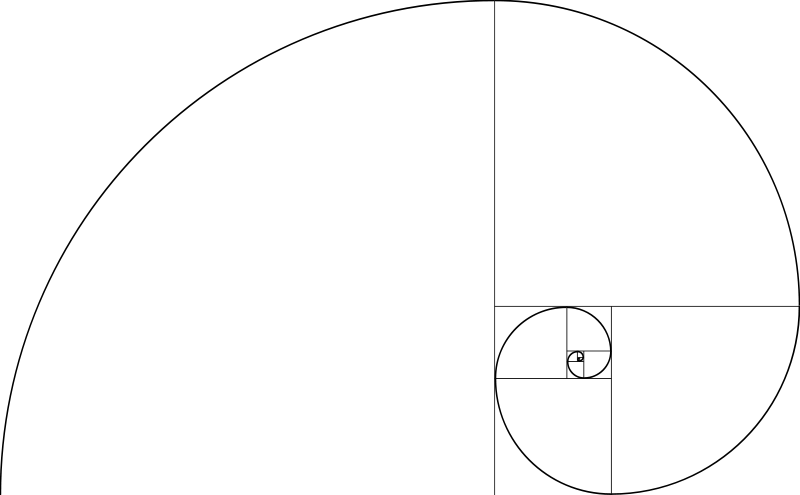
Fibonacci dizisinden elde edilen fibonacci spirali de aşağıdaki gibi bir şeydir ve sanat eserlerine de sık sık uyarlanır (hatta fotoğraf kompozisyonu hakkında mürekkep yalamışlık taslamak isteyen kişilerin ilk ortaya attığı “üçte bir kuralı” da, köşeleri birleştirilerek bu spiralin oluşmasını sağlayan karelerin en sonuncusunun tüm karelerin kapladığı alana oranından gelir, aşağıdaki şekle baktığınızda ne demek istediğimi kolayca görebilirsiniz).

Bu spiral şöyle oluşur: en küçük iki karenin kenarı 1 ve 1 birimdir, bir büyüğünün kenarı 2 birimdir, bir sonraki karenin kenarı 3 birimdir, bir sonrakininki 5’tir, bu bu şekilde 8, 13, 21, 34 diye devam eder. Daha sonra bu kareleri birleştirdiğinizde yukarıdaki spiral ortaya çıkar.

Konudan konuya atlamacılık: Bir yılı aşkın süredir beraber çalıştığım lab teknisyenimiz, maestromuz, gönlümüzde taht kurmuş tatlı insan Amanda Alba (1, 2), önümüzdeki hafta hayırlı bir nedenle ile New York’a taşınıyor (Columbia Üniversitesi’ne kabul edildiği için, gidişine adam gibi üzülemedik bile). Küçük bir veda partisi vesilesi ile arkadaşları olarak dün onun French Quarter’daki evinde bir araya geldik. Ben de bir kaç fotoğraf çektim olay mahallini belgelemek adına. Çektiklerimden bir tanesi de aşağıdaki fotoğraf:

Yakınımda olan ve fotoğraf ile ilgilenen kişiler kadraja giren objelerin geometrik ilişkilerine fena halde itina gösteren bir insan olduğumu söylerler arada bir. Çoğunlukla fotoğrafı çekerken çok fark etmesem de daha sonra çektiğim fotoğrafları incelerken bu konuya iç güdüsel şekilde çok özen gösterdiğimi ben de fark ediyorum açıkçası.

Öte yandan geometrik ilişkilerin insanların bir fotoğraftan aldıkları mesajı çok değiştirdiğini, Barthes’in fotoğraf düşünürlerine kazandırdığı bir terim olan Punctum‘u ortaya çıkarma ya da güçlendirme konusunda rol aldığını da düşünüyorum.

Örneğin yukarıdaki fotoğrafı daha sonradan incelediğimde çok hoşuma gitti ve çekmiş olduğuma çok sevindiğim fotoğraflardan birisi oldu. Bununla beraber sadece ben değil, bir kaç kişinin fotoğrafla ilgili beğenilerini işittim. Fakat fotoğraftaki diğer kişi olan Dr. Alexander Stoyanov’un -daha önce bir çok fotoğrafımı görmüş olmasına rağmen- bu fotoğrafa dair attığı “senin fotoğraf konusunda bu kadar yetkin bir insan olduğunu bilmiyordum” içerikli e-postası bardağı taşıran son damla oldu. “Bir saniye” dedim kendi kendime. Neden bu fotoğrafı beğenmek herkes için bu kadar kolay olmuştu? Bu işin içinde bir iş mi varmıştı? Tam o sırada aklıma fibonacci dizisi geldi (hehe, evet, geliyor öyle arada bir aklıma). Fibonacci dizisinin meşhur spiralini fotoğrafa uyarlamaya karar verdim. Sonuç etkileyici idi, çünkü neredeyse bütün görsel ögeler ya fibonacci spirali tarafından ziyaret ediliyor ya da kendilerine kareler içerisinde anlamlı bir yer buluyorlardı:

Duygu fotoğrafı gördüğünde şöyle demişti:

Direkler! Aa çatılar. Katedral! Sokak tabelası bile orada. Süper olmuş!

Bir kişinin kendi fotoğrafını bu şekilde anlamaya çalışması biraz komik duyuluyor, farkındayım. Bunu başkalarının yapmasını bekleyecek kadar meşhur filan olmadığım için iş başa düşüyor, mazur görün :) Fakat beni fotoğrafa dair en çok etkileyen şey direkler olmuştu. Siz fotoğrafı izlerken nelere hangi sıra ile dikkat ettiniz bilemiyorum ama Duygu’nun son gördüğü direk en soldaki direk olmuştu. Acaba algı gerçekten fibonacci spiralinin dağılımı ile oranlı bir şekilde mi ayrıntılara odaklanıyor bilemiyorum. Fotoğrafı çekerken bunlara dikkat etmemiştim, fakat bu kadrajı seçmiş olmam işin içinde doğal bir takım geometrik güdülerin olduğunu düşündürdü bana.

Sonra dedim ki, “bir de herkesin -diğer fotoğraflarıma haksızlık edercesine- beğendiği bir fotoğrafım üzerinde deneyeyim, bakayım ne çıkacak”. Bu çıktı:

Sonra dedim ki “Kendi fotoğraflarını bırak, bir de başkasının fotoğrafına bak”. Hemen Erdal Kınacı’nın bu gün paylaştığı ve görür görmez “kıskanılası fotoğraflar” klasörüme eklediğim fotoğrafı geldi aklıma, aldım baktım, bir de ne göreyim:

</p>

© Erdal Kınacı</td> </tr> </tbody> </table>

Peki. Daha fazla uzatmayacağım. Bu yazıdan çıkan fikirler şunlar, üzerlerinde düşünmenizi rica ediyorum:

  • Fibonacci dizisi inanılmaz bir şey.
  • Fibonacci dizisi ile elde edilen geometrik oranlar ile insanları bir görüşte etkileyen fotoğraflardaki objelerin yerleşimleri arasında enteresan bir ilişki var. Fotoğrafçının çekerken bunu dikkate aldığını söylemek güç iken sonuçların örtüşüyor olması düşündürücü.
  • Erdal Kınacı’nın İstanbul’da fotoğraf çekmesi bir an önce yasaklanmalı, hatta sınır dışı edilmeli (bu durumda “şehir dışı” edilmesi daha yerinde olabilir). Daha fazla fotoğraf çekerse Haydarpaşa Vapur İskelesi, Balıkçı ve Martı fotoğrafı çekerek hayatını devam ettiren fotoğrafçı güruhunun kendilerine, başkalarına veya Erdal Kınacı’ya zarar vermeye teşebbüs etmesi ihtimali söz konusu.