Neden Bazı Lensler Diğerlerinden Daha İyi?
Bu sorunun yanıtını vermek çok kolay değil. Bir yerinden başlamak için ise bence evvelâ lens dediğimiz şeyin ne iş yaptığını ve bunu nasıl yaptığını iyice anlamak gerek.
Bu yazı ile amacım işleri fazla karmaşıklaştırmadan mevzu hakkında bir fikri olsun isteyenlere yardımcı olmaya çalışmak. Ama beni altruizmin pençesine düşmüş psikopat bir iyilik perisi sanıp kendinizi suçlu hissetmemeniz için bu yazıyı sizler için olduğu kadar kendim için de yazdığımı ifade etmek isterim. Kafamda dağınık şekilde duran şeyleri bir araya toparlıyorum, bunu da alenen yaparak belki başkalarına da faydası olur diye umuyorum (böyle buyurdu Zerdüşt).
Bazı lenslerin diğerlerinden daha iyi olmasının ardında elbette birçok faktör var. Fakat bu faktörlerin hepsi bu yazının ilgi alanına girmiyor. Ben işin sadece modelleme ve hesap kitap kısmı ile ilgili bir şeyler yazacağım. Siz de okursanız genel kültür olması için okumalısınız, çünkü daha fazlasını vaat ettiğimi düşünmenizi istemem.
***
Bir lensin optik olarak ne kadar iyi olduğu hakkında konuşmaya başlamak için, kendisinden beklenen şeyleri yerine getirirken emekçi lens kardeşlerimizi ne tür problemlerin beklediğini anlamalı ve kendimizi onların yerine koyabilmeliyiz.
Başlamadan evvel yazı boyunca lenslerin içinde varlık gösterdiğimiz ve üç boyutlu olan gerçek dünyayı, iki boyutlu ve çoğu durumda gerçeğinden daha küçük olan bir yüzeyde yeniden ifade etme problemi ile başa çıkmaya çalıştıklarını hatırlamanızı istiyorum (hatta şu an durup bunun üzerine düşünmek ve anladıktan sonra devam etmek için çok doğru bir an olabilir). Tahmin edebileceğiniz gibi bu yüzey analog makineler için film, dijital makineler için ise ise, sensör.
Optik şakaya gelecek bir konu değil. Zira optik ve lensler ile ilgili bilgilerimiz fotoğraf makinelerinin ortaya çıkışından çok daha önceye dayanıyor.
Neden çok daha önceye dayanıyor?
Çünkü fotoğraftan çok önce de optik düzenekler yoğun olarak kullanılıyordu.
Kim kullanıyordu?
Kafamızı her konuda şişiren mendebur fizikçiler kullanıyordu.
Ne için kullanıyorlardı?
Elbette yaptıkları teleskoplar ile fezaya bakıp insanların kafasını allak bullak etmek, zaman zaman da din adamlarını çileden çıkarmak için kullanıyorlardı :(
Düşünecek olursanız bir teleskobun yaptığı şey ile bir lensin yaptığı şey arasında çok ciddi bir fark yok: ikisi de ışığı optik bileşenler yardımı ile bir noktada toplamaya çalışıyorlar. Ve ne yazık ki ikisi de bunu sadece belirli bir isabet ile başarabiliyorlar. Dolayısıyla bu günün fotoğraf makineleri için üretilen lenslerinin karşılaştığı problemler uzun zaman evvel araştırılmış, varlığı tespit edilmiş problemler. Bu yazı içerisinde çok çok yüzeysel bir şekilde o problemlerin nereden geldiğinden, neden var olduğundan bahsetmeye çalışacağım.
Devam etmeden önce bu kısmın başında sorduğum soruyu yineleyip yanıtlayayım: Bir lensten yerine getirmesi beklenen şey nedir?
İdeal bir lensin oluşturacağı projeksiyona dair üç temel beklentimiz var:
- Görüntülenen objenin üzerindeki bir noktadan gelen her bir ışık ışını film/sensör yüzeyi üzerinde sadece bir noktada toplanmalı.
- Görüntülenen obje yüzeyi optik eksene dik ise, görüntü de dik olmalı, yani açılar korunmalı.
- Gerçek obje ve objenin lens tarafından oluşturulan görüntüsü birbiri ile aynı olmalı.
Teoride beklentimiz bunlar olsa da, gerçekte lenslerin oluşturan mercekler ışığı kırarken görüntüde kaçınılmaz bir takım hatalar oluşmasına sebep oluyorlar. Dolayısıyla gerçek hayatta hiçbir lens yukarıdaki üç beklentiyi de tam olarak yerine getiremiyor. Meydana gelen bu hataların her birine “bozulma” (ing.: abberation) deniyor.
***
Bir lensin oluşturduğu görüntü ile gerçek görüntü arasındaki farklara sebep olan toplam yedi çeşit bozulma var.
Bunlardan ilk beş tanesi Seidel bozulmaları olarak da bilinen monokromatik bozulmalar (yani ışığın dalga boyundan (renklerden) bağımsız bozulmalar). Diğer ikisi ise kromatik bozulmalar (yani farklı dalga boylarına aynı şekilde muamele edilememesine bağlı bozulmalar). Bunlara az sonra tek tek değineceğim.
Özetle mercekler ışığı kırarak gerçek dünyayı iki boyutlu düzlemde yeniden oluşturuyorlar, ama bu sırada bir takım optik bozulmalar meydana geliyor(muş). Neden ve nasıl, bilmiyoruz henüz.
Peki. Konuya biraz farklı bir tarafından yaklaşmak için ani bir manevra yapıyorum (ve o sırada uyuyanlarınız kafalarını cama çarpıyorlar (hehe)).
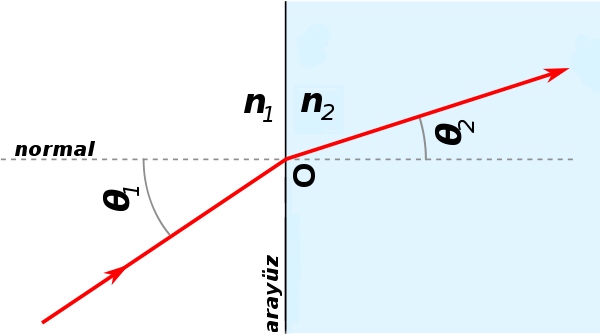
Willebrord van Royen Snell isimli bir amcamız 1800’lü yıllarda ortaya daha sonra Snell kanunu olarak anılacak bir teori atıyor:
|
Snell kanunu yukarıdaki gibi n1 ve n2 farklı kırılma indislerine sahip ortamlardan birisinden diğerine geçen ışık ışınının kırılma açılarının arasında şu şekilde açıklanabilecek bir bağıntı olduğunu söylüyor:

|
Fizikçilerin kafası kuantum mekaniği, izafiyet, yoğun madde fiziği, astrofizik filan ile çok meşgul olduğu için hâlâ geçerliliğini koruyan bu kanun mercek tasarımı için teorik olarak yeterli (yani kırılma indisini bildiğim bir madde kullanarak bir mercek tasarlar, ona girecek her ışık ışınının nasıl kırılacağını, mercek arkasında nereye düşeceğini sadece bu formülden yola çıkarak hesaplayabilirim). Fakat tahmin ettiğiniz gibi pratikte bazı engeller var…
Bu aklımızın bir köşesinde dursun şimdi.
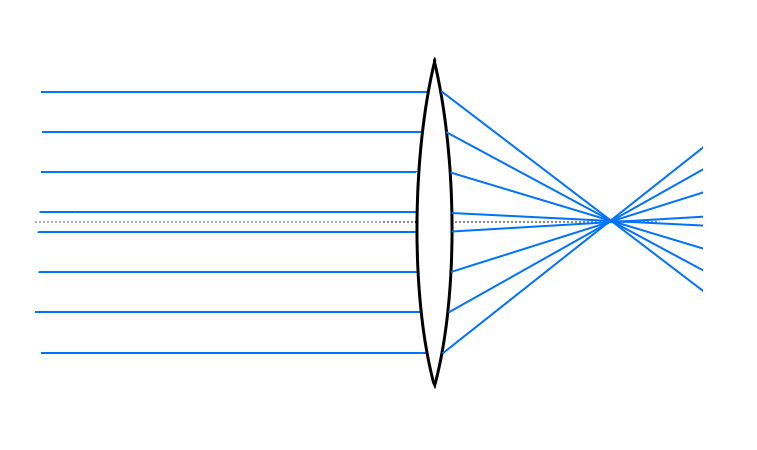
Herkesin aşağıdaki, bütün ışık ışınlarının tek bir noktada toplandığı illüstrasyonu hatırlayacağını tahmin ediyorum:
|
Bize böyle anlatılmış olmasına rağmen bu iş gerçekte pek de böyle olmuyor, bir mercekten kırılan ışık ışınları hiçbir zaman tek bir noktada toplanmıyor. Işığın mercek ile yukarıdaki toz pembe dansı, eğitim sisteminin bize attığı kazıklardan bir diğeri :(
Işık ışınlarının yukarıdaki formasyonu bir yakınsamadan ibaret. Bu yakınsamanın literatürdeki ismi de “paraxial approximation” (=”Gauss approximation”, “Gauss yakınsaması”).
Bir merceğin davranışının yukarıdaki gibi olmaya en çok yaklaştığı durum, mercek yüzeyine gelen ışık ışınlarının her birinin geliş açısının 10°’den daha düşük olduğu durum. Bu da Snell kanunundaki θ’nın 10°’den küçük değerleri için sin(θ) ≈ θ kabulünü yapmakta çok çok büyük bir sakınca olmamasından ileri geliyor. Fakat gerçek hayatta ışık ışınları küresel yüzeylerden kırıldığı zaman tek bir noktada toplanmak yerine, örneğin yukarıdaki örnek için, aşağıdaki gibi bir davranış sergiliyorlar:
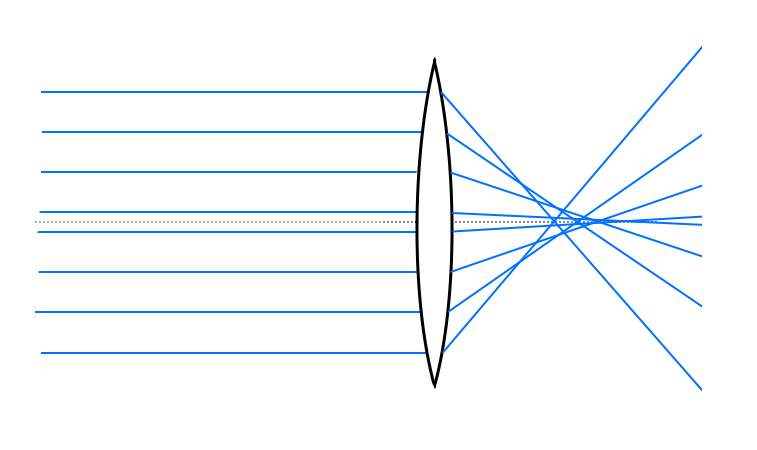
|
Yani bozulmalar aslında kimsenin hatası olmayıp merceklerin bir işe yaramaları için yüzeylerinin dışbükey -ya da içbükey- olmasının doğal bir sonucu (lenslerin birçok merceğin bir araya gelmesinden oluşmasının nedeni de işte buradan geliyor: her bir bileşenin varlık sebebi kendisinden önceki lenslerin sebep olduğu bozulmaları düzeltmek).
***
Snell kanununu ile bir mercek yüzeyine ulaşan her ışık ışınının nasıl kırılacağını ve tam olarak nereye düşeceğini hesaplamak mümkün iken formülde sin(θ) ≈ θ kabulünü yaptığımızda optik hataların olmadığı, gerçekle ilgisi olmayan bir mercek davranışı öngörüyoruz. Halbuki sin(θ)’nın gerçek değerini hesaplasak bir merceğe gelecek ışık ışınlarının nasıl bir rota izleyeceğini tam olarak modelleyebilir, tüm optik hataları da görebilirdik. Fakat bunu yapmak biraz zor. Çünkü verilen herhangi bir θ için sin(θ)’nın gerçek değerini hesaplamak hiç de kolay bir iş değil (bunu yapmak için sin fonksiyonunun Taylor serisi açılımını kullanıyoruz ve bu seri sonsuz sayıda eleman içeriyor (bkz: aşağıdaki seri açılımı)). Bu nedenle, Snell kanunu daha basit matematik ifadelere indirgenemeyen çetrefilli bir hesap gerektiriyor. Bir diğer deyişle, Snell kanununda sin(θ) yerine θ koymak kolay bir hesap fakat gerçekle ilgisi olmayan bir sonuç verirken, sin(θ) yerine sin(θ)’nın gerçek değerini koymak çok gerçekçi bir sonuç veriyor, fakat çok zor bir hesap ile beraber geliyor.
Halbuki Snell’in sin(θ)’larını, Gauss’un yaptığı gibi θ kabul etmek ile sin(θ)’nın gerçek değerini hesaplamak arasındaki bir toplam ifadesine dönüştürebilsek işlerimiz çok daha kolay olurdu. “Hem görüntünün kırılmadan sonra nasıl olacağının yeterince isabetli bir hesabını yapabilecek, hem de hesaplaması kolay bir formül olsa tadından yenir miydi şimdi“… İşte Philipp Ludwig von Seidel bey amcanın da kafasını 1800’lü yılların ortalarında kurcalayan soru tam olarak buymuştu (miştili geçmiş zaman kipine dikkatinizi çekmek isterim).
Çakal Seidel kişisi şöyle diyor: “Ben bir sin(x) fonksiyonunu şöyle güzelinden bir seriye açsam, verilen bir x için sin(x) değerini hesaplamak için şu şekilde sonsuza uzayan nur topu gibi bir ifadem olurdu“:

|
Seidel devam eder: “Gauss kırılma açısını hesaplamak için bu açılımın yalnızca ilk ifadesini (first order approximation) ‘sonuç’ kabul ediyor ve tüm hesaplarını onun üzerinden yapıyordu, ben sadece ilki yerine mercek üzerine düşen her ışının kırılma açısını hesaplamak için ‘ilk iki ifadeyi’ kullansam acaba gerçeğe ne kadar yakınsarım (third order approximation)“.
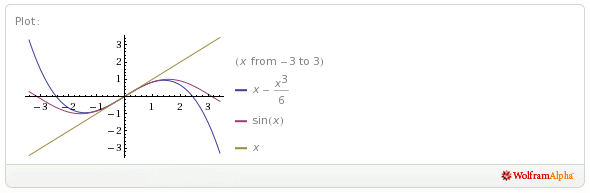
Hem sin(x) fonksiyonunun kendisini, hem tek başına x değerini, hem de sin(x) seri açılımının ilk iki ifadesini çizdirince bu yaklaşımın sin(θ) ≈ θ kabul eden Gauss yakınsamasından ne kadar daha iyi olduğunu görmek çok daha kolay oluyor:
|
(Bu noktada “madem seri açılımının ilk iki ifadesi bu kadar yakınsıyor, neden ilk üç ifadesi ya da daha fazlası ile yapılmıyor hesaplamalar?” diye sorabilirsiniz. Bunun yanıtı da dahil ettiğimiz her ifade için başa çıkmak zorunda kaldığımız polinomların hızla karmaşıklaşıyor olması ( muhtemelen çok daha isabetli yöntemlere başvuruyorlardır, fakat optik teorisi ile ilgili bilgim sınırlı olduğu için “şöyle yapıyorlardır” diyemiyorum)).
Sonuç olarak Seidel bu üçüncü dereceden ifadeyi kullanarak mercekler üzerinde çalışmaya ve davranışlarını analiz etmeye başlıyor. Yaptığı deneylerde karşılaştığı bozulmaları da 5 grupta topluyor. Bununla da kalmıyor, bu 5 monokromatik hatanın verilen herhangi bir mercek için ne kadar ciddi olduğunu bulmak için sayısal bir metrik de sunuyor. Açıklamaya çalıştığım durumda okuyan bir kişinin alacağı toplam verim, anlaşılması için açıklamak gerekecek olan wavefront teorisi ve co-efficiency hesabının nasıl yapıldığını anlatmaya çalışma külfetine değmeyeceği için bu konuyu es geçiyorum. Fakat buradan hatırlanması gereken şey Seidel’in birçok merceğin bir araya gelmesi ile oluşan optik düzeneklerin toplam hatalarının hesaplanması için her bir ifadenin bir hataya karşılık geldiği bir polinom da geliştirmiş olduğu (hatta ZEMAX kullanarak mercekleri bir araya getirip bu sistemin toplam bozulma indislerini hesaplayabiliyorsunuz mesela)(bununla beraber bu gün Leica, Carl Zeiss, Sigma, Nikon gibi çok büyük lens üreticileri yeni bir lens modellerken, lens içindeki tüm merceklerin oluşturduğu optik sistemin sebep olduğu bozulmayı mümkün olan en yaklaşık sonuçlarla hesaplamak için Seidel polinomu yerine kendi araştırmaları ile şirket sırrı haline gelmiş güncel Zernike polinomlarını kullanılıyorlar muhtemelen, fakat Seidel işin teorisini anlamak ve “first order approximation”dan “third order approximation”a geçmenin neden gerekli olmuş olduğunu anlamak için daha güzel bir patika sunuyor bence).
Nihayet Seidel’in bozulmalarından bahsetmeye hazırım.
***
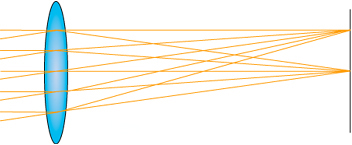
Literatürde Seidel’in 5 Bozulması olarak da geçen monokromatik bozulmalara başlamadan önce ideal durumu örnekleyeyim (görüldüğü üzere farklı açılarla gelen ışınlar başarı ile tek bir noktada odaklanıyorlar):
|
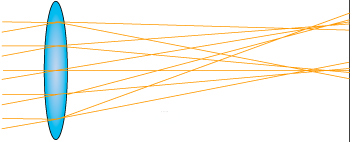
- Küresel bozulma (“spherical aberration“): Küresel bozulmanın kaynağı merceğin merkezine gelen ışınların, merceğin kenarlarına gelen ışınlardan daha az kırılması sonucu odak noktasının lens ekseni boyunca dağılmasıdır. Görüntünün şeklini bozmamakla birlikte keskinliğini bozar. Dolayısıyla küresel bozulmanın yeterince düzeltilmediği optik sistemlerin oluşturduğu imajlar flu olur. Fotokritik’te kafanızı kırarlar. Aşağıdaki görüntüye bakıp tam olarak kafanızda canlandırmanız için gerçekten üç boyutlu düşünmelisiniz. Eğer yeterince iyi düşünürseniz, tüm problemin merceklerin, kenarlarına gelen ışık ışınlarına farklı davranmasından kaynaklı olduğunu görebilirsiniz. İşte bu yüzden diyafram kısıldıkça fotoğraflar netleşir. Çünkü diyafram kısıldıkça kenardan gelen ışık ışınlarının daha büyük bir kısmı resmin dışında kalır (hatta şöyle bir video buldum, çok güzel açıklıyor durumu: http://www.youtube.com/watch?v=E85FZ7WLvao (videoda tek bir noktadan çıkan ışık ışınlarının merceğin farklı noktalarından geçtikten sonra nasıl da tek bir noktada buluşamadığına dikkat edin)). Bu yüzden diyafram maksimum açıklığında iken keskin fotoğraflar çekebilen lensler modellemek çok zor.
|
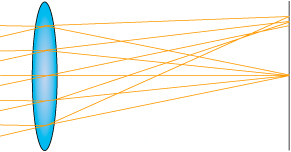
- Koma (“coma“): Seidel’in beş bozulmasından ikincisi… Koma, merceğin optik ekseni üzerinde veya yakınında olan objelerden gelen ışınların adam yerine konmaması anlamına geliyor. Eksen üzerindeki veya yakınındaki objelerden gelen, yani amiyane bir tabir ile, merceğin “baktığı” tarafta olan objeler net bir projeksiyon oluştururken merceğin baktığı yönde olmayan fakat yine de projeksiyon oluşturabilen görüntüler bozuk oluyorlar. Biraz düşünürseniz bunun geniş açı bir lenste, telefoto bir lenste yarattığından daha ciddi bir probleme neden olduğunu hissedebilirsiniz. YouTube’de bu anlatmaya çalıştığım şeyi anlatan eden pek güzel bir video buldum: http://www.youtube.com/watch?v=EXmaY2txEBo. Şu imaj da koma bozukluğunu güzel örneklemiş, özellikle videoyu izledikten sonra daha çok anlam ifade edecektir. Koma bozukluğunun yumuşak ve tatlı bokehlerin en büyük düşmanı olduğunu da söylemeli. Bir lensin bokehinin güzelliği, optik sistemin tasarlanması esnasındaki hesapların keskinliği ve detayı ile doğrudan ilintili.
|
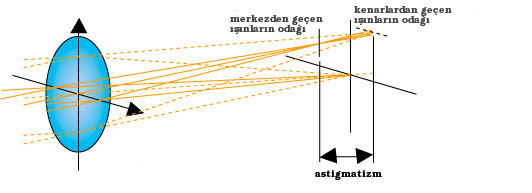
- Astigmatik fark (“astigmatism“): Aşağıdaki şekle bakıp da astigmatik farkın ne olduğunu anlayabilenin alnında öperim. Çünkü ben ona baktım, baktım, hiçbir şey anlamadım. Ama size güzelce açıklamanın bir yolunu buldum. O yüzden figürü boş verip bunu dikkatle okuyun (figürü de ibret-i alem olsun deyyu kaldırmayacağım): Astigmatik fark, temelinde merceğe yatay ve düşey eksenler üzerinden gelen ışınların farklı noktalarda odaklanmaları olan bir bozukluktur; mesela bir artı simgesinin düşey olan çizgisi net iken yatay olan çizgisinin flu olması gibi etkileri olur. Bu bir artı işareti değil de bir dairenin olduğu durumda dairenin odak noktasında eliptik görünmesine neden olur.
|
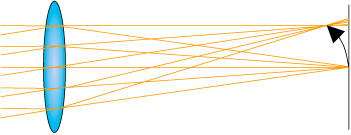
- Saha eğriliği (“curvature of field“): Küresel bozukluk, koma ve astigmatik farkın aksine bu hatada bir noktadan çıkan ışık ışınları bir noktada toplanırlar. Fakat görüntünün odaklandığı yer merkezden kenarlara doğru gidildikçe aşamalı olarak odağın düşey ekseninden uzaklaşır. Dolayısıyla merkezden uzaklaştıkça keskinlik aşamalı olarak azalır. Kenarlarda maksimuma varır. Aşağıdaki imajı hayalinizde canlandırın ve o siyah oka parmağınızla pıt diye vurup onu merceğin ekseni etrafında 360 derece döndürdüğünüzü hayal edin. Onun dönüşünü hayal ederken, siyah ok boyunca ilerleyen odak noktasının bir küre kapağına benzediğini gözünüzde canlandırabilirsiniz. Fakat film ya da sensör yüzeyi dümdüzdür. Kırırım ben böyle düz sensörü.
|
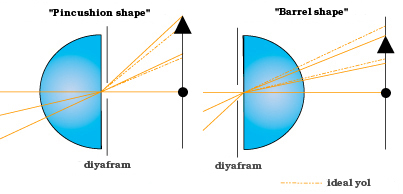
- Deformasyon (“distortion“): Bu hataların her biri adım adım düzeltiliyor. Örneğin saha eğriliğinin test edilip düzeltilmesi için küresel bozulmanın düzeltilmiş olması gerekiyor. Bu bağlamda en son problem deformasyon problemi oluyor. Bu evren bize sona kalanın çoğunlukla dona kaldığını öğrettiği için şanslıyız. Çünkü neden lenslerin bir çoğunda deformasyonun bir vazgeçilmez olduğunu hemen anlayabiliyoruz (adamlar “eeah ilk dördünü düzelttik, yeter. İrfan, ara Mehmet abini ‘lens hazırmış’ de” diyorlar). Deformasyonun iki ana türü var, pincushion deformasyonu ve barrel deformasyonu (ilki görüntünün bu şekilde bozulmasına sebep olurken, ikincisi bu şekilde bozulmasına sebep oluyor). Sebebi ise merceğin merkezinde ve kenarlarında farklı büyütme etkileri gösteriyor olması. İlkinde kenarlara doğru gidildikçe büyütme etkisi artarken (dolayısıyla ortaya içbükey bir görünüm çıkarken), ikincisinde büyütme etkisi merkezden uzaklaştıkça azalıyor (dolayısıyla ortaya dışbükey bir görünüm çıkıyor) Örneğin Nikon’un 18-200mm lensinde bu problemi çözemedikleri gibi bazı odak uzaklıklarında bu iki bozukluğun hibrit birlikteliğine rastlamak da mümkündü. Bu yüzden kimseye tavsiye etmediğim gibi ilk fırsatta kurtulmuştum. Bu mevzuları öğrendikçe insan neden o kadar geniş aralıklı bir zoom lensin üstün bir performans ortaya koyamayacağını daha net görüyor.
|
Seidel bey amcanın Gauss optiğinin sin(θ) ≈ θ kabulünü bir kenara bırakıp sin fonksiyonunun Taylor serisi açılımındaki ikinci polinomal ifadeyi de kırılma açısı hesabına dahil etmesi ile ortaya çıkardığı doğal mercek bozukluklarının monokromatik olanları bunlardan ibaret. Fakat bir de temelinde ışığın farklı dalga boylarının mercekten geçerken farklı miktarlarda yavaşlaması olan kromatik bozukluklar var.
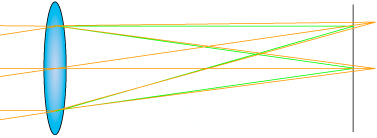
Bunlardan ilki uzunlamasına kromatik bozukluk (“longitudinal chromatic aberration“). Uzunlamasına kromatik bozukluk, şeklin yine göstermeyi harika bir biçimde beceremediği gibi bazı dalga boyları kırılmanın ardından odak noktasının gerisine ya da ilerisine düşemesi durumu:
|
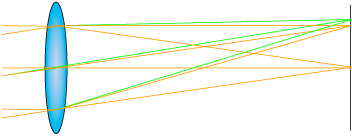
Diğeri de enine kromatik bozukluk (“leteral chromatic aberration“). Bu bazı dalga boyları kırılmanın ardından odak altına, üstüne, sağına, soluna düşmesi durumu (aslında objenin kare içerisinde nerede olduğuna göre eksenden büyüyen dairesel bir dağılım ortaya koyuyor).
|
Kromatik bozukluklar karşımıza şu ya da şu ya da özellikle şunun gibi renk ayrımı problemleri çıkarıyorlar. Ayrıca YouTube’de kromatik bozukluğun nasıl gerçekleştiğini gösteren harika bir diğer video buldum: http://www.youtube.com/watch?v=yOR4WHgRfvI. Bu videoda da görebileceğiniz gibi kromatik bozukluk da diğer bir çok bozukluk gibi diyaframın açık olduğu durumlarda daha etkili oluyor.
***
Peki. Bazı lenslerin diğerlerinden daha iyi olmasının tek sebebi bu hesapların isabetli olması mı? Elbette hayır.
Yukarıdaki hataları barındırmayan optik sistemler modellemek için hesapların kesinliği gibi önemli olan diğer iki hususun da malzeme ve inşa kalitesi olduğu aşikâr.
Fakat ben kendi adıma işin metalurji mühendisliği kısmının günümüzün önde gelen lens üreticileri arasında çok çok değişiklik gösterdiğini pek sanmıyorum. Bu gün bir lensin kalitesi üzerindeki en büyük etkenin, birden fazla merceğin bir araya gelmesi ile oluşturulan optik sistemi modellerken, ortaya çıkacak toplam bozulmayı doğru tespit edebilmek için kullanılan polinomlar olması olasılığı çok yüksek bana göre (Leica, Zeiss, Nikon, Canon, Sigma gibi büyük lens üreticilerinin Snell yasasının 5’inci dereceden hatta 7’inci dereceden polinomlarının da modelleme hesaplarına dahil edilmediğini, sadece hiç değiştirilmemiş Zernike ya da Seidel polinomlarından faydalanarak modelleme yaptıklarını düşünmek naiflik olurdu sanırım). Optik konusunda çalışmak, problemi evrimsel algoritmalarla ifade edip var olan lens tasarımlarını iyileştirmeye çalışmak ne zevkli olurdu diye düşündüm bu yazıyı yazarken. Bu konularda benden çok daha bilgili insanlar olduğuna şüphem yok. Denk gelirlerse deneyimlerini ve bilgilerini aktarırlar belki.
Ben de bu yazıyı yazmaya karar verdiğim sırada boş durmayıp Twitter’dan insanlara “neden bazı lensler diğerlerinden daha iyi?” diye sordum. Çok isabetli yanıtlar geldi, aşağıdakilerin hepsi öyle veya böyle doğru:

|

|

|

|

|

|

|

|
Eren Türkay ve Yalçın Aydın ise 140 karakter içinde acımayıp 12’den vurmuşlar (insan 140 karakterde bu kadar anlatıldığını görünce bu yazıyı yazdığına utanıyor):

|

|
Fakat bazı lenslerin neden diğerlerinden daha iyi olduğuna dair en doğru yanıt Gökçen’den geldi ve kendisi bu günün en birincisi oldu.
Bu, şu ana kadar biriktirdiğim birincilik tellerinden kendisi için hazırladığım birincilik tacı:

|
Bu da Gökçen’e birincilik tacını getiren yanıtı:

|
Evet. Çok doğru. Zira İslami usullere uygun kesilmeyen merceklerden yapılan lensleri kullanmak pek caiz değildir.